Vimos na postagem "Posições e deslocamentos escalares" que é importante conhecermos as grandezas Posição escalar e deslocamento de modo a classificarmos a existência ou não de um movimento.
Embora essas grandezas possam nos mostrar a ocorrência de um movimento, elas por si só não bastam para classificá-lo.
Em todo movimento a maneira como os deslocamentos são realizados é muito importante. Imagine que em uma roda de conversa dois amigos digam que viajaram 200 km, cada um em um percurso diferente e gastando tempos diferentes para isso.
Se o objetivo da conversa era falar sobre dirigir rápido ou não, você já deve imaginar que, para isso, devemos analisar não só a distância percorrida por ambos, mas também o tempo que cada um levou para cumprir o seu trajeto.
Essa associação entre os deslocamentos e seus respectivos tempos é exatamente o que a grandeza física velocidade nos informa.
Assim, podemos definir a velocidade como sendo a razão entre os deslocamentos efetuados e seus respectivos tempos.
Matematicamente falando,
onde
ΔS = deslocamento realizado,
Δt = tempo gasto para realizar o deslocamento.
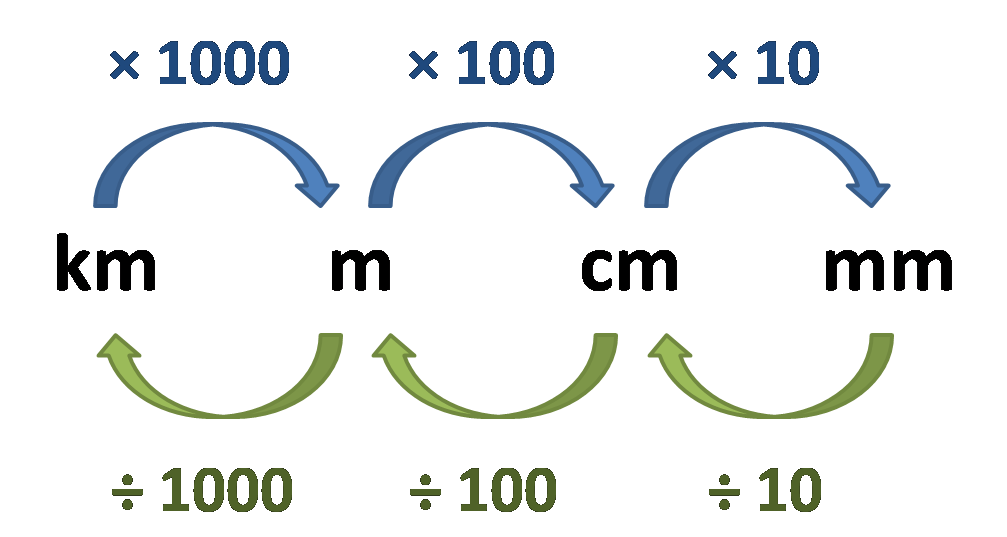
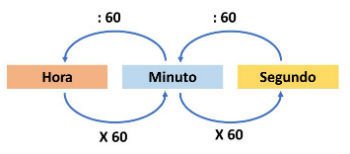
Uma coisa que devemos ter sempre em mente e´que, de uma forma geral, as velocidades são calculadas em m/s (metros por segundo) ou km/h (quilômetros por hora). Assim, quando nos depararmos com tempos ou distâncias em unidades que não são as que usaremos para o cálculo da velocidade deveremos convertê-las antes de realizar os cálculos.
Lembre-se:
Fig. 1 - Conversão entre unidades de comprimento e distância.
e
Fig 2 - Conversão entre unidades de tempo.
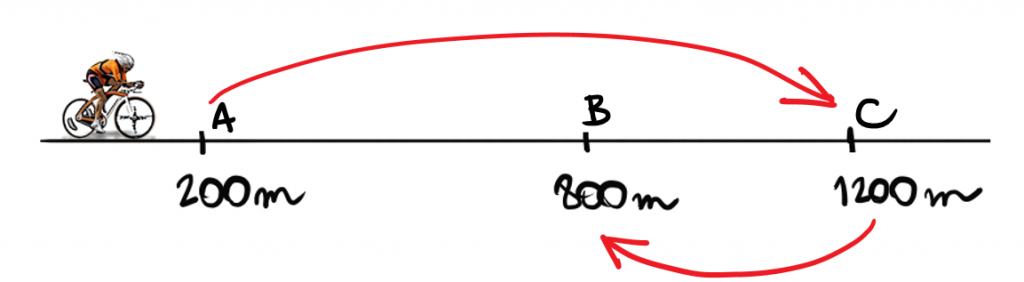
Considere que o ciclista da imagem acima vá do ponto A para o ponto C em 4 min e que ao chegar em C ele volte até o ponto B, gastando de C para B, 2 min.
Podemos calcular sua velocidade em diferentes trajetos.
a) Quando ele vai de A para C:
- Seu deslocamento foi de 1000 metros
- Ele levou 4 min, o que corresponde a 240 segundos (4×60)
- Sua velocidade foi de
V = 1000 ÷ 240 = 4,16 m/s (metros por segundo).
b) Quando ele vai de C para B:
- Seu deslocamento foi de -400 metros
- Ele levou 2 min, o que corresponde a 120 segundos (2×60)
- Sua velocidade foi de
V = -400 ÷ 120 = -3,33 m/s (metros por segundo).
c) Em todo o movimento, ou seja, saindo de A, passando por C e chegando em B:
- Seu deslocamento foi de 1400 metros
- Ele levou 6 min, o que corresponde a 360 segundos (5×60)
- Sua velocidade foi de
V = 1400 ÷ 360 = 3,88 m/s (metros por segundo).
Uma vez que obtemos suas velocidades em cada trajeto, sabemos que o seu trajeto mais rápido foi entre A e C. Já de C para B ele foi um pouco mais devagar.
Repare que em nossa conta, a última velocidade encontrada foi de 3,88 m/s, que é um valor intermediário entre os 4,165 m/s iniciais e os 3,33 m/s do segundo trajeto.
Essa velocidade é chamada de velocidade média, pois ela não leva em conta que durante o trajeto a velocidade tenha variado. Ela é calculada apenas sobre o deslocamento total e o tempo total gasto.
Assim, uma velocidade média não representa o valor exato da velocidade em cada parte de um trajeto, apenas uma média das velocidades desenvolvidas.